Isto porque o homem, descrevendo um movimento circular uniforme, é acelerado em direção ao centro da Terra. A fôrça necessária para produzir esta aceleração é suprida pela fôrça gravitacional, F_g. Se esta fôrça, F_g, não se opusesse à fôrça da balança, resultaria numa aceleração de 9,8 m/s². Mas ela é anulada, em parte, pela balança, limitando a aceleração para 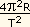. Portanto, a fôrça da balança para cima, F_b, que é oposta a F_g para baixo, deve ser tal que a resultante para baixo tenha um módulo que forneça uma aceleração de . 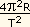A fôrça resultante dessa aceleração é: 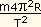. Logo, F_g-F_b = 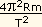= = 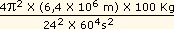3,4 newtons.

O peso aparente do homem no equador, medido na balança, deve ser 3,4 newtons menos do que os 980 newtons lidos no polo. Isto representaria uma "perda" de 0,35%.

b) Se o homem não exercesse fôrça alguma sôbre uma balança no equador, seria necessário que: 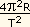= = 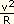g. Então:

v² = Rg = 6,4 X 10⁶ m X 9,8 m/s², e v = 7,9 X 10³ m/s.

O período T', necessário para esta velocidade, seria:

T' = 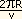= = 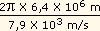5,1 X 10³ s = 1,4 horas.

c) A velocidade determinada na parte (b) e a velocidade real serão inversamente proporcionais aos respectivos períodos:

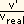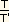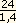= = = 17.



PROBLEMA 22

Duas estrelas que compõem uma estrela dupla, bastante afastadas de qualquer outra massa considerável, giram em órbitas circulares, permanecendo sempre separadas pela mesma distância.

(a) Esboce suas órbitas, se elas têm massas iguais;

(b) Se uma tem o dobro da massa da outra.

(c) Qual a razão entre os raios de suas órbitas, em cada caso?

Este problema, também um tanto difícil, auxilia os alunos a pensar a respeito do centro de massa - um dos assuntos do próximo capítulo. O problema ilustra que, quando um par de corpos gira, um ao redor do outro, realmente ambos se movem. Portanto, ainda que frequentemente se diga que a Lua gira ao redor da Terra uma vez por mês, na verdade, ambas giram em tôrno de um centro comum de massa, uma vez por mês.

Para este problema, o importante é observar que as duas estrelas sempre permanecem separadas por uma mesma distância. Isto significa que, onde quer que estejam os seus centros de rotação, eles devem ser os mesmos, e as estrelas devem ter o mesmo período de rotação. Atualmente sabemos, de modo geral, que a força de atração da estrela 1 pela estrela 2 é igual à força de atração da estrela 2 pela estrela 1, e esta é a causa da aceleração centrípeta de cada uma delas:

F = = =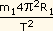

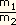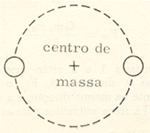
a) Se as estrelas têm massas iguais, o centro em torno do qual elas giram é o ponto médio entre elas. Suas trajetórias são círculos em tôrno de centro de massa. Desde que são iguais as distâncias ao centro de massa, ambos os círculos têm o mesmo raio.

Principal
Guia do Professor
Anterior
Próxima