PROBLEMA 11


(a) A que altura deve estar um satélite, movendo-se no plano do equador, para permanecer sôbre um mesmo lugar, no equador da Terra? Um modo de obter a resposta consiste em comparar êsse satélite com a Lua, que dista 59,5 raios terrestres do centro da Terra, e leva 27 dias para contorná-la.

(b) Qual a aceleração do satélite na direção da Terra?

(c) Usando a lei do inverso do quadrado e o valor de g na superfície da Terra, determine o campo gravitacional à altura do satélite. Compare com a resposta obtida em (b).

a) O satélite permanecerá imóvel relativamente a um ponto sôbre a superfície da Terra, se seu período T fôr o mesmo que o da Terra, aproximadamente, um dia (realmente, 365/366 do dia).

O raio da órbita do satélite pode ser encontrado pela terceira lei de Kepler e pela informação de que a Lua está a 59,5 raios terrestres do centro da Terra, e gira uma vez em cada 27 (27,3) dias. Seja R_s e R_l os raios da órbita do satélite e da órbita da Lua, e T_s e T_l seus períodos.

=

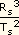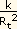Rs = ( 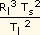)1/3 =

= = 6,6 raios da Terra.

Como o raio da Terra é 6,4 x 10⁶ m, R_s = 6,6 x 6,4 x 10⁶ m = 4,2 x 10⁷ m. A altura do satélite, acima da superfície da Terra, seria 4,2 x 10⁷ m - 6,4 x 10⁶ m = 3,6 x 10⁷ m.


b) O satélite seria acelerado para a Terra com um valor:

a = (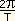) ²R = 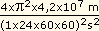= 0,22 m/s².


c) A fôrça devido à gravidade e, portanto, a aceleração devido à gravidade é proporcional a 1/R². Assim, a aceleração g, na altura do satélite e g, na superfície da Terra, estão relacionadas, como se seguem:

gs = 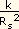; gt =

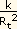gs = 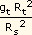= 9,8 m/s2 x ( 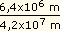)2 = 0,23 m/s2

Portanto, vimos na parte (b) que se pode determinar a aceleração a paltir de R e T, sem usar a lei do inverso do quadrado da fôrça, e, na parte (c), que podemos determinar a aceleração a partir de g, na superfície da Terra, utilizando a lei do inverso do quadrado. Êstes foram os dois métodos empregados por Newton, para calcular a aceleração da Lua
(veja no texto, páginas 60-62).


PROBLEMA 12

Um satélite circunda a Terra em 98 minutos, à altura média de 500 km. Calcule a massa da Terra. As massas dos planêtas são realmente calculadas pelos movimentos dos satélites, e uma das razões para colocar em órbitas satélites artificiais da Terra é que se deseja obter um valor melhor para a massa da Terra. Como foi estabelecido na Seção 22-10, G = 0,667 X 10^-10 m³/kg.s².

A terceira lei de Kepler estabelece que R³/T² é uma constante para os movimentos de todos os satélites, mas não especifica a natureza da constante.

Empregando a lei da gravitação universal, podemos igualar a fôrça centrípeta à fôrça gravitacional sôbre o satélite (se a órbita fôr conhecida). Logo, se designarmos a massa do satélite por m_s, e a da Terra por m_t,

= G

mt = .

Principal
Guia do Professor
Anterior
Próxima