| Substituindo, |
R = 6,37 x 106 m +
5,00 x 105m = 6,87 x 106 m, e
T = 98 x 60 s = 5,88 x 103 s
4 2
x (6,87 X 106 m) 3 2
x (6,87 X 106 m) 3 |
mt = ------------------------------------------------- =
0,667 x 10-10 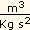 x (5,88 x 103s)2 = 5,5 x 1024 Kg.
x (5,88 x 103s)2 = 5,5 x 1024 Kg.
PROBLEMA 13
(a) Sendo T o período de um satélite que circula pouco
acima da superfície de um planeta cuja densidade média
é 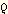 ,
mostre que ,
mostre que 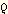 T2
é uma constante universal. T2
é uma constante universal.
(b) Qual o valor desta constante?
a) Como no Problema 12, podemos escrever:
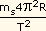 = G
= G 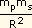 ,
e mp = ,
e mp = 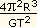 .
.
Se R  Rp,
raio do planeta, podemos escrever: Rp,
raio do planeta, podemos escrever:
mp = 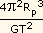 .
. |
Mas mp = 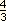
 Rp3 Rp3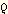 ,
onde ,
onde 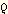 = densidade.
= densidade.
Portanto,
Isolando o 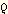 T2,
obtemos: T2,
obtemos: 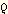 T2
= 3 T2
= 3 / G,
o que demonstra a proposição acima, visto que G é
uma constante universal. / G,
o que demonstra a proposição acima, visto que G é
uma constante universal.
b) Desenvolvendo,
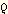 T2
= T2
= 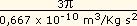 = 1,41 x 1011 Kgs2/m3.
= 1,41 x 1011 Kgs2/m3.
PROBLEMA 14
Calcule os períodos de um satélite numa órbita
próxima à superfície: (a) da Terra. (b) do Sol.
Esta é um sequência simples do Problema 13, mas pode
também ser feito diretamente.
Pelo Problema 13, sabemos que 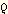 T2
é uma constante universal para um satélite movendo-se
próximo à superfície de qualquer corpo. T2
é uma constante universal para um satélite movendo-se
próximo à superfície de qualquer corpo.
Assim,
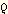 sTs2
= sTs2
= 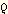 tTt2
= 1,41 x 1011 Kg s2/m3. tTt2
= 1,41 x 1011 Kg s2/m3.
Como 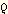 t
= 5,5 x 103 Kg/m3, Tt = ( t
= 5,5 x 103 Kg/m3, Tt = ( 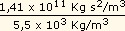 ) 1/2 = 5,1 x 103 s = 85 min.
) 1/2 = 5,1 x 103 s = 85 min.
Tomando 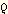 s s
 1,4 x 103
Kg/m3, Ts = ( 1,4 x 103
Kg/m3, Ts = ( 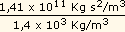 ) 1/2
) 1/2  104s
104s  167 min.
167 min.
Considerando diretamente, a aceleração centrípeta
na superfície da Terra é 9,8 m/s2 =
4 2R
/ T2 . Rt = 6,4 x 106 m. Entretanto, 2R
/ T2 . Rt = 6,4 x 106 m. Entretanto,
T = 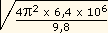 = 2
= 2 x 0,81 x 103
= 5,1 x 103 s. x 0,81 x 103
= 5,1 x 103 s.
Em geral, agora: 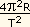 = G
= G 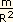
Logo, T2  R3/m. O raio do Sol é
R3/m. O raio do Sol é
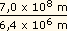 = 1,1 x 102
= 1,1 x 102 |
vêzes o da Terra. A massa do Sol é
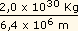 =
= 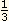 x 106
x 106 |
vezes a da Terra. Consequentemente, o período do movimento
do satélite, na superfície do Sol, é 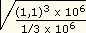
 2 vêzes
o seu período na superfície da Terra, isto é,
104 segundos. 2 vêzes
o seu período na superfície da Terra, isto é,
104 segundos.
Principal
Guia do Professor
Anterior
Próxima
|