PROBLEMA 15
Determine o peso de um homem de 100 Kg nos planetas com as seguintes
massas e raios:
| Marte |
6,4 x 1023 Kg |
3,4 x 106 m |
| Terra |
6,0 x 1024 Kg |
6,4 x 106 m |
| Júpiter |
1,9 x 1027 Kg |
7,2 x 107 m |
Desde que o peso é simplesmente a força de gravidade sobre
o homem de 100 Kg, empregando
P = F = 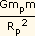 , , |
e substituindo a massa e o raio correspondentes de cada um dos três
planêtas, determinamos que o homem de 100 kg pesa 360 newtons
em Marte, 980 newtons na Terra, e 2400 newtons em Júpiter.
PROBLEMA 16
Um rapaz de 70 kg está a um metro de uma moça de 60 kg.
Calcule a fôrça de
atração (gravitacional) entre êles.
F = 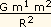 |
F = 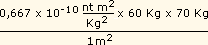 |
F = 2,8 x 10-7 newtons. |
Esta força de atração é somente uma pequena
fração do peso da moça (F/P = 4,8 x 10-10).
Obviamente, deve ser algo mais que a gravidade o que exerce atraçào
mútua entre rapazes e moças!
PROBLEMA 17
Determine a atração gravitacional entre dois átomos
de uma molécula de hidrogênio.
Este problema simples, envolvendo a lei da gravitação
universal, tem por finalidade mostrar a insignificância das
forças gravitacionais na escala atômica.
Ainda que a maior parte dos alunos provavelmente se recorde que a
massa de um átomo de hidrogênio foi determinada no Capítulo
8, (1,67 x 10-27 Kg), muitos bons alunos claudicarão,
quando tentarem encontrar um valor para R, a distância entre
dois átomos na molécula de hidrogênio. Os dotados
de boa memória podem se lembrar de que, no Capítulo
7, Seção 13, a dimensão linear de um átomo
foi determinada como sendo cêrca de 1 Angstron, e no Capítulo
8, seção 4, aprendemos que a molécula de hidrogênio
tem, aproximadamente, um comprimento duas vezes maior que a largura.
Daí, podem concluir que os centros dos átomos estão
separados de, aproximadamente, 1 Angstrom. Ao designar este problema,
talvez você queira dizer aos alunos que o indício da
distância está nos Capítulos 7 e 8 ou, simplesmente,
deseje fornecer-lhes o número, R  10-10 m
10-10 m
F = 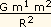
F =
 1,9 x 10-44
newtons 1,9 x 10-44
newtons
Para comparação, a força elétrica entre
um próton e um elétron, no átomo de hidrogênio,
é cerca de 10-8 newtons, aproximadamente, 1036
vezes maior! As forças gravitacionais são completamente
desprezíveis nos problemas atômicos.
PROBLEMA 18
( a) O diâmetro de um planêta é o dôbro do
terrestre e sua massa é seis vêzes maior do que a da
Terra. Qual a razão entre o campo gravitacional na sua superfície
e o campo gravitacional na superfície da Terra?
(b) Qual a razão das densidades dos dois planêtas?
Este problema refere-se à dependência entre a massa e
a distância, na lei da gravitação. Ele conduz
a um raciocínio mais abstrato (isto é, trata-se de um
problema mais algébrico do que numérico) e fornece a
prática com escala.
Principal
Guia do Professor
Anterior
Próxima |