22 - 5. Kepler.

Johannes Kepler, nascido em 1571, estava em nítido contraste com Tycho Brahe. Tycho possuía tremenda habilidade e destreza mecânica, mas interêsse relativamente pequeno em matemática. Kepler era desajeitado como experimentador mas era fascinado pelo poder da matemática. Era semelhante aos antigos gregos em sua reverência pelo poder dos números e interessava-se por quebra-cabeças relativos a número e tamanho.
Depois de haver aprendido os elementos de astronomia, Kepler ficou obcecado com o problema de encontrar uma esquema numérico para o sistema planetário. Êle escreveu: "Eu refletia com tôda a energia de meu espírito sôbre êsse assunto". Devotou sua vida à análise das tabelas das posições planetárias que Tycho lhe havia deixado. Enfrentando o problema de traduzir as observações de Tycho Brahe em descrições matemáticas dos movimentos planetários, Kepler agiu como qualquer cientista de hoje que tenta explicar dados experimentais em têrmos de leis matemáticas simples, e não apenas mediante tabelas de números. Com leis matemáticas podemos não só reproduzir os dados observados como predizer os resultados de observações que ainda não tenham sido feitas. Ademais, as leis matemáticas são mais fáceis de lembrar e de comunicar do que meras tabelas de números. Em seu primeiro livro, Kepler descreveu suas tentativas de entender por que havia precisamente seis planêtas no sistema solar.
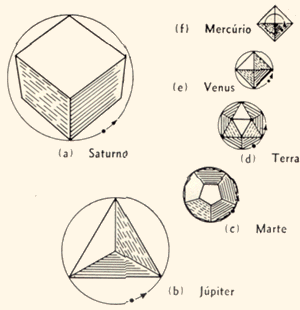
		22.8 - A lei de Kepler das órbitas planetárias baseava-se nos cinco sólidos regulares. De acôrdo com a lei, uma esfera de raio igual ao da órbita de Saturno circunscreve um cubo (a). Uma esfera Inscrita nesse cubo tem ralo igual ao da órbita de Júpiter. Em (b) mostra-se a esfera da órbita de Júpiter, com um tetraedro inscrito. Uma esfera inscrita no tetraedro dá o raio da órbita de Marte. Em (c) a esfera relativa a Marte tem um dodecaedro inscrito. Uma esfera inscrita nêle dá a órbita da Terra (d). Podemos continuar nesse processo de inscrição alternada de esferas e sólidos regulares usando o icosaedro (vinte lados) e o octaedro. Êsses nos darão as órbitas de Vênus (e) e de Mercúrio (f), que está numa esfera inscrita dentro do octaedro. Kepler considerava os cinco sólidos como preenchendo os intervalos entre as órbitas planetárias. Como há somente cinco sólidos regulares, Kepler acreditava que poderia haver apenas cinco planetas.

Estabeleceu uma ligação entre as seis órbitas e os cinco sólidos geométricos regulares (*) (Fig. 22-8). A partir desta construção obteve razões entre os raios que concordavam muito bem com os valores então conhecidos das órbitas planetárias.

Kepler ficou extasiado. Escreveu: "O intenso prazer que sentí com essa descoberta não pode ser descrito em palavras. Não me importo mais
com o tempo despendido; não me incomodo de nenhum trabalho; não fugí a nenhum trabalho de verificação, dias e noites despendidos em cálculos, até que pudesse ver se minhas hipóteses concordavam com as órbitas de Copérnico, ou se minha alegria devia desvanecer-se no ar."

A relação entre os raios das órbitas planetárias é típica da espécie de resultado que Kepler esperava obter com os dados de Tycho. Ocorre frequentemente, entretanto, que mesmo a mais bela correlação entre dados não tem qualquer significado profundo para explicar a natureza das coisas. Hoje, essa descoberta de Kepler está inteiramente esquecida. Seu sistema está destruído pelo fato de haver mais de seis planêtas. Mas o sétimo só foi descoberto muito anos depois de sua morte.

Kepler descobriu outras relações matemáticas, que sobreviveram ao teste de observações posteriores. Começou sua grande análise dos dados de Tycho com um estudo exaustivo do movimento de Marte. Que espécie de curva teria Marte percorrido durante os vinte anos de observações de Tycho? As observações dos movimentos planetários eram feitas necessàriamente da Terra.

(*) Por corpo sólido regular entende-se um corpo simétrico com faces planas iguais. Só podem ser construidas cinco espécies de corpos sólidos regulares.

Principal
Parte III
Anterior
Próxima