Marte se moveria segundo uma curva mais simples se imaginássemos a Terra em repouso, ou se imaginássemos que ela está em movimento como acreditava Copérnico? Kepler adotou a idéia comperniciana de que a Terra gira em redor de seu eixo, ao mesmo tempo que percorre uma órbita em tôrno do Sol. Seguindo a tradição, êle tentou primeiro um sistema de círculos que se moviam sôbre outros círculos para obter órbitas possíveis. Fez inúmeras tentativas cada uma envolvendo longos e laboriosos cálculos. Tinha de traduzir as medidas de Tycho, do ângulo entre Marte e as estrêlas fixas, para definir a posição do planêta no espaço em relação a um Sol fixo, em tôrno do qual se movia a própria Terra.

Depois de cêrca de setenta tentativas, usando órbitas do tipo "círculo excêntrico", Kepler encontrou um esquema que concordava muito bem com os fatos. Depois, para seu desânimo, verificou que essa curva, quando prolongada além do domínio dos dados que havia usado, discordava de outras observações da posição de Marte, feitas por Tycho.

A discordância entre os dados de Brahe e os cálculos de Kepler eram de cêrca de 8/60 de grau (êste é o ângulo percorrido pelo ponteiro menor de um relógio em 0,02 segundo). Não poderia Tycho ter cometido êsse pequeno êrro? Não poderia o frio de uma noite de inverno ter entorpecido seus dedos, ou confundido suas observações? Kepler conhecia os métodos de Tycho e seu cuidado escrupuloso. Tycho nunca teria cometido nem êsse pequeno êrro. Assim, baseado nos dados de Tycho, Kepler rejeitou as curvas que tinha construido. Que tributo era isto à memória de seu mestre!

Dizendo que "Sôbre êsses oito minutos poderia ainda construir uma teoria do Universo", Kepler recomeçou. Desprezando a antiga e estimada crença no movimento uniforme, considerou possíveis variações na velocidade de um planêta quando êste se move em tôrno do Sol. Fez então sua primeira grande descoberta. Verificou que uma linha tirada do Sol ao planêta descreve áreas iguais em tempos iguais. Isto veio a ser conhecido como a segunda lei de Kepler (Fig.22-9).

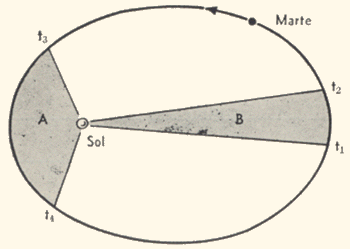
	22 - 9 - Lei de Kepler das áreas iguais. Marte percorre sua órbita com velocidade variável movendo-se mais rapidamente quando está mais próximo do Sol. Kepler verificou que, para intervalos de tempo iguais, t2 - t1 = t4 - t3, as áreas varridas pela linha que vai do Sol ao planeta eram iguais. (Área B = Área A). No desenho o alongamento da elipse foi exagerado para ilustrar mais claramente a lei das áreas iguais.

Após a descoberta de sua segunda lei, Kepler abandonou finalmente suas tentativas de construir os movimentos planetários a partir de combinações de movimentos circulares uniformes e começou a tentar várias ovais como órbitas possíveis. Depois de muitos cálculos mais complicados, conseguiu finalmente um de seus resultados mais importantes: a assim chamada primeira lei. Verificou que cada planêta move-se numa órbita elítica, estando o Sol num dos focos. Imagine-se o deleite de Kepler. Após tantos anos de esfôrço, tinha finalmente encontrado uma curva simples que descrevia o movimento dos planêtas.

Kepler pôs-se, então, a procurar uma conexão entre o tamanho da órbita de um planêta e seu período, isto é, o tempo de uma revolução do planêta em tôrno do Sol. Após muitas tentativas, obtêve a relação precisa que procurava: para todos os planêtas, a razão entre o cubo do raio da órbita e o quadrado do período é a mesma (*). Uma vez calculada esta razão, a regularidade era flagrante (Ver Tabela 1). A constância da razão R³/T² é chamada a terceira lei de Kepler.

Com êste triunfo, Kepler escreveu: "...o que dezesseis anos atrás eu exigia, com uma coisa a ser procurada...o motivo pelo qual procurei Tycho Brahe...por fim eu trouxe à luz e reconheço sua verdade além de minhas esperanças mais apaixonadas... A sorte está lançada, o livro está escrito para ser lido agora ou pela posteridade. Não me preocupo - êle bem pode esperar por um leitor durante um século, como Deus esperou seis mil anos por um observador".

(*) O raio R de uma órbita é definido como a média aritmética entre a maior e a menor distância do Sol ao planêta. Como as órbitas planetárias não são muito diferentes de círculos, a distância do Sol a qualquer ponto da órbita bastará para a maioria dos fins.


Principal
Parte III
Anterior
Próxima