Já discutimos a influência de um campo magnético sobre um condutor retilíneo percorrido por corrente. Nesse caso nos preocupamos apenas com o trecho do fio que estava no campo. O resto do condutor, que completava o circuito ligando-se a uma pilha, não estava sujeito a forças de origem magnética, porque estava fora do campo.
Estudaremos agora o caso em que um condutor que forma um circuito fechado percorrido por corrente está todo dentro de uma região em que há campo magnético.
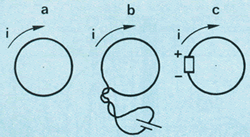
Um fio condutor, com a forma indicada na figura 22, percorrido por uma
corrente i, é chamado espira circular de corrente.
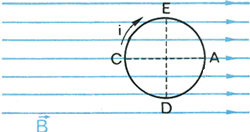
Imagine uma espira de corrente colocada num campo magnético uniforme
paralelo ao seu plano, como mostra a figura 23.
 |
| figura 22 |
 |
| figura 23 |
Q33 - Indique nos pontos A, C, D e E da figura 23 a direção e o sentido de percurso da corrente.
Q34 - Qual a direção e o sentido da força que aparece no ponto A da espira?
Q35 - Qual a direção e o sentido da força que aparece no ponto C?
Q36 - Qual o módulo da força nos pontos D e E?
Q37 - Qual a relação entre os módulos da força
em A e em C?
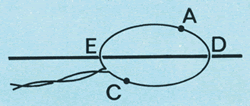
Imagine que a espira seja suspensa num suporte horizontal, pelos pontos
D e E. Imagine também que, na ausência de campo
magnético, ela esteja equilibrada nesse suporte (veja figura 24).
 |
| figura 24 |
Q38 - O que deve ocorrer com a espira assim suspensa, quando colocada
num campo magnético uniforme, paralelo ao seu plano?
Nessas condições, será que somente os pontos A
e C ficarão sujeitos à ação de uma força?
Já vimos que em D e E a força é nula; como será então a força no trecho situado entre esses pontos?
Nessas regiões, i não é perpendicular a 
;
para determinar o módulo de 
,
devemos utilizar a expressão
F = i 
B sen  . |
À medida que nos aproximamos de E ou D, o ângulo
entre i e
vai decrescendo; assim, a força, que depende de sen
também decresce.
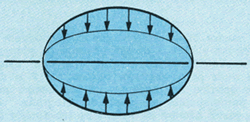
As forças que aparecem sobre os vários trechos da espira
estão representados na figura 25.
 |
| figura 25 |
Note que em cada um dos semicírculos a força tem o mesmo sentido.
Q39 - Qual deve ser o valor da resultante de todas as forças que agem sobre a espira?
Para calcular a força total que age em cada semicírculo, são necessárias técnicas matemáticas um pouco mais complexas. Não faremos isso agora.
Estudaremos uma configuração parecida, considerando uma espira retangular, pois nesse caso o cálculo fica muito simplificado e as conclusões serão semelhantes.
Você vai inicialmente observar o que se passa, fazendo uma experiência.
Tome um fio condutor dobrado de modo a formar um retângulo (figura 26); o fio deve ser isolado externamente (pode ser de cobre envernizado). A corrente deve percorrer esse dispositivo, como está indicado na figura, sem que haja contato nos pontos C e D, em que o fio é superposto.
 |
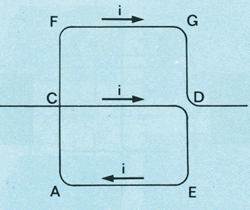| figura 26 |
Monte esse dispositivo num suporte e estabeleça um campo magnético
uniforme, paralelo ao plano do dispositivo. Esse campo magnético
pode ser obtido, com boa aproximação, se você usar dois
ímãs de barra como mostra a figura 27.
 |
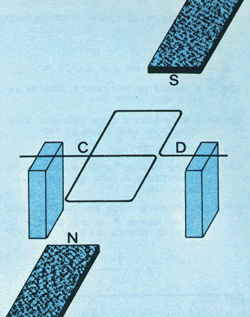| figura 27 |
Feche o círculo, ligando C e D, respectivamente, aos terminais positivo e negativo de uma pilha.
Q40 - Descreva o que ocorre na experiência, no instante em que a pilha é ligada, e indique, na figura 28, as forças que aparecem em cada trecho do dispositivo.
 |
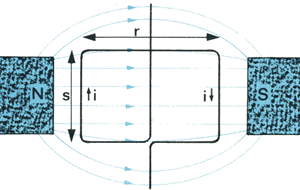| figura 28 |
Se conhecermos os valores de
e de i, podemos ainda calcular a intensidade da força nos
trechos AE e FG.
Sejam r e s os comprimentos dos lados do retângulo
(figura 28); então, F = isB para os lados perpendiculares
a , e F =
0, para os lados paralelos a.
Quando uma força produz ou tende a produzir rotação em torno de um eixo fixo, é conveniente exprimir a situação por meio de uma grandeza vetorial chamada conjugado (ou torque) da força em relação ao eixo.
Em nosso caso, obtém-se o módulo do conjugado, multiplicando o módulo da força pela distância entre o ponto de aplicação da força e o eixo de rotação. O conjugado, devido à força em AE, tem intensidade
O conjugado correspondente à força em HG é
Como os dois conjugados têm por efeito fazer o retângulo girar no mesmo sentido, o torque total sobre o retângulo será:
= 1 +
2 |
ou |
= F.s |
Substituindo a expressão de F em função de B e i, teremos:
|
= i.s.r.B |
mas s.r é a área A do retângulo, então:
|
= i A B |
(6) |
Essa expressão, que permite calcular o conjugado, vale também para uma espira plana de forma qualquer. Essa generalização pode ser demonstrada e verificada experimentalmente.
Q41 - Escreva a expressão de
para uma espira de raio r.
A expressão
= iAB é válida no casos em que a direção
do campo magnético é paralela ao plano da espira. Se a direção
do campo não for paralela ao plano da espira, o torque terá
um valor diferente e, no caso particular em que essa direção
é perpendicular ao plano da espira, o torque será zero.
Em resumo, um condutor de qualquer forma, percorrido por corrente e imerso
num campo magnético uniforme, fica sujeito a um conjunto de forças.
A resultante de todas essas forças é nula e, dependendo da
forma do fio e de sua orientação em relação
ao campo, pode estar sujeita a um torque.
Respostas
 |
|
 |
|
 |
|
|
|